[논문]
- CcDPM: A Continuous Conditional Diffusion Probabilistic Model for Inverse Design
- AAAI 2024
- Citations: 4
- [https://ojs.aaai.org/index.php/AAAI/article/view/29647]
0.Abstract
- cGANs - single-point design problems에서 promising results
- Single-point: one performance requirement under one working condition
- Categorical space 가정
- CcGANs - Vicinal Risk Minimization(VRM)도입했지만, 여전히 multi-point design problem 다루지 못함
- Multi-point: multiple performance requirements under multiple working conditions
- vicinal loss의 계산 복잡성으로 training 오래걸림
- CcDPM - engineering design area와 VRM을 diffusion에 처음 도입한 model
- multi-point design sampling 도입 ⇒ multi-point design problems 다룰 수 있음
- k-d tree - In, training process, vicinal loss의 계산 시간 단축 & 2-300배의 훈련속도 가속화
- synthetic problem & three real-word deign problems ⇒ SOTA GAN보다 outperforms
1. Introduction
- continuity of input working condition을 adapt하기 위해 loss ft에 VRM 도입
- Vicinal loss in the training process의 시간을 줄이기 위해 k-dimensional tree 도입
2. Background
- Inverse design problems은 conditional generative problems으로 여길 수 있음
- VRM - empirical risk minimization(ERM)의 alternative rule
- Assume - sample point가 vicinity의 다른 samples과 label 공유
- ERM - continuous scenario에서 사용 X
- CGAN & conditional diffusional models에 사용
- each distinct label에 대한 충분한 samples 필요 but condtion이 continuous하면 각 label에 대한 충분한 samples확보 어렵
- ⇒ discriminator의 loss ft에 vicinal loss based on VRM 도입
3. Methodology
Problem Definition
- $x$ - $R^d$ ⇒ design variables
- ${w_{c_1},w_{c_2}, ..., w_{c_m}}$ ⇒ m개의 working conditions
- ${y_1, y_2, ...,y_m}$ ⇒ 각 $w_{c_i}$에 대응하는 performance requirements
- $y_i$ - $R^K$, K개의 성능지표
- Inverse design problem - given {${w_{c_1},w_{c_2}, ..., w_{c_m}}$}, {${y_1, y_2, ...,y_m}$}일 때, $x$ 찾기
- 각 $w_{c_i}$에서 $y_i$의 performance 만족해야함
- Conditional probability distribution을 solving하는 문제

- dataset D = {$(x^1, w^1_c, y_1),...,(x^N,w^N_c,y^N)$}
- $x^i$는 under working condition $w^i_c$에서 performance $y^i$
- condtional dist $q$를 approximate하는 $p_\theta$ 학습 ⇒ our target
Loss Function of CcDPM
- performance requirements의 dist는 continuous ⇒ empirical dist 사용 unreasonable

- vicinal loss - KDE를 이용한 marginal dist $p(w_c,y)$의 smooth estimation
- Dirac delta대신 KDE를 이용하여 $p(u)$를 smooth
- ⇒ Soft vicinal estimate(SVE) - new estimate for $p(x,u)$
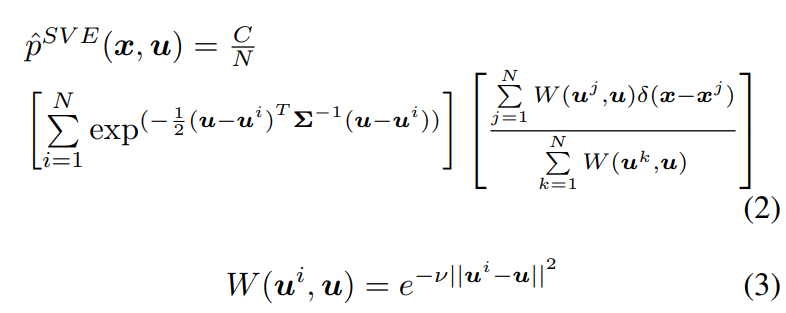
- $\nu$ - Hyper-parameter & C - constant
- $p^{SVE}$ - dataset $(x,u)$쌍의 smoothed empirical dist
- $\exp\left(-\frac{1}{2} (u - u^i)^T \Sigma^{-1} (u - u^i)\right)$ - 각 $u^i$에 대해 $u$의 값이 얼마나 가까운지 측정하는 gaussian kernel
- $e^{-\nu |u^i - u|^2}$ - $u^i$와 $u$의 유사성 측정 function
- 유클리디언 distance 기반의 exponential 감소 ft ⇒ 서로 가까울수록 큰 weight
- $\nu$ - 감소율 조절하는 hyperparameter
⇒ gaussian kernel * weight term
- loss ft

- $\epsilon$ - diffusion model에서 추가되는 noise
- $\epsilon'$ - condition에 추가되는 noise
- 모든 sample pair (i,j) 계산
⇒ DDPM의 simple loss에 soft vicinity weight 추가
Training Process


- loss 계산시, k distance 이내의 모든 dataset을 탐색
- $O(N)$ → k-d tree를 이용하여 $O(log$ $n)$으로 이웃 탐색 가능
- $C$를 이용하여 k-d tree를 먼저 construct
- $t,u^i$를 sampling 후, $u^i$에 gaussian noise 추가하여 $\hat u^i$를 생성
- k-d tree사용하여 $\hat u^i$의 $\kappa$개의 가까운 이웃 search ⇒ $D_i$ 얻음
- threshold $\kappa$
- $\hat u^i$와 $D_i$의 sample하나 $D_i^j$를 이용하여 weight $W(\hat u^i, u^{i_j})$ 계산
- $\epsilon_\theta(x^{i_j}, \hat u^i, t))$와 $W$를 이용하여 최종 loss 계산
Multi-Point Design Sampling
- Training - $p_\theta(x|w_c,y)$ ⇒ one working condition input에서만 학습
- $\hat q$ - Markovian noising process 새롭게 정의 ⇒ multiple condition에서 sampling 가능
- Reverse process


- In generation, Working condition is known & $w_c$와 x는 independent
- Assume - 동일 x에서 다른 $w_c$에 대한 y들은 서로 독립
- Sampling method with estimator

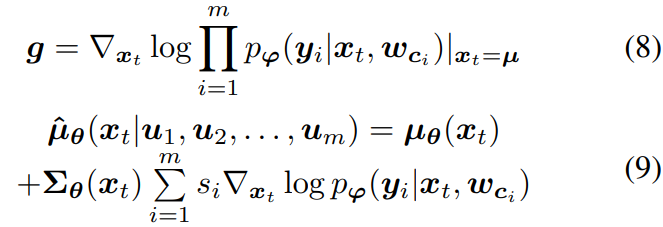
- $p_\psi(y_i|x_T,w_{c_i})$ - 계산 어렵 & 추가적인 model 필요
- ⇒ estimator free sampling method 사용
- ⇒ CG의 sampling 방법과 동일
- Estimator free sampling
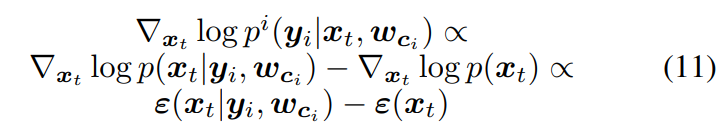

- $\epsilon_\theta(x_t)$ - uncondtional output of the model
- $s_i$ - guiding scaling of specific performance under specific working condtions
- 최종 $\hat\epsilon$구한 뒤, DDPM or DDIM의 sampler와 동일한 방식으로 sample $x_{t-1}$ 생성


[정리]
- In training, t와 $u^i$를 sampling 후 vicinal loss 계산하여 condtion하나에 대한 $\theta$ update
- In Sampling, t step에서 uncondition과 모든 m개의 condition의 $\epsilon_\theta$를 계산 후 Sum
- ⇒ 해당 $\epsilon$으로 DDPM/DDIM의 sampling 방식 사용
'Paper Review > 2D Diffusion Model' 카테고리의 다른 글
| [논문 리뷰] Palette: Image-to-Image Diffusion Models (0) | 2025.03.21 |
|---|---|
| [논문 리뷰] CCDM: Continuous Conditional Diffusion Models for Image Generation (0) | 2025.03.21 |
| [논문 리뷰] CFG: Classifier-Free Diffusion Guidance (2) | 2025.03.21 |
| [논문 리뷰] CG: Diffusion models beat gans on image synthesis (0) | 2025.03.21 |
| [논문 리뷰] DDIM: Denoising Diffusion Implicit Models (2) | 2025.03.18 |



