[논문]
- Classifier-Free Diffusion Guidance
- NeurIPS 2021
- Citations: 3,518
- https://arxiv.org/abs/2207.12598
0. Abstract
- Guidance can be indeed performed by a pure generative model without such a classifier
- ⇒ Classifier-free guidance
- cond/unconditional diffusion model을 jointly train
- cond/unconditional score estimates를 combine하여 quality & diversity의 trade-off를 attain
1. Introduction
- Classifier guidance
- A technique to boost the sample quality of a diffsuion model using an extra trained classifier
- diffusion model’s score estimate과 classifier의 log probability의 gradient를 mix
- ⇒ Diffusion model에서 “low temperature” sampling 가능
- classifier gradient의 strength를 변화하여 IS(Precision) & FID(Recall)의 trade off 가능
- Classifier의 문제점
- Complicates training pipeline
- Unable to plug in to pretrained classifier ⇒ noisy image를 classification하는 model 필요
- Can be interpreted as gradient based adversarial attack to boost up specific metrics
- Classifier의 gradients를 활용하여 sampling
- FID, IS와 같이 이미지 model을 활용하는 metric에서 gradient based adversarial attack과 같이 특정 class 방향으로 이동시키는 방식으로 성능 향상한 것이 아닌지 알 수 없음
- ⇒ 단순히 Diffusion이 좋은 것이 아니라 이미 성능이 좋은 GAN과 비슷한 방식의 classifier graident를 사용하여 향상시킨 것이 아닌지 의문점 발생
- ⇒ 문제점 해결하기 위해 Classifier-free guidance 제시
- Complicates training pipeline
- Classifier-free guidance
- any classifier 사용 X
- cond/unconditional diffusion model의 score estimates를 jointly trained
- mixing weight ⇒ FID/IS trade off를 attain
⇒ pure generative diffusion models도 high fidelity samples가 가능하다는 것 demonstarte
2. Background
- “Understanding Diffusion”의 수식
- Classifier Guidance


- Classifier-Free Guidance
- Classifier Guidance


- VDM 논문의 conditional diffusion 수식 사용
- [Continuous Diffusion models]

- $x=x_0$
- $z_\lambda=x_t$ with continuous $t$
- $p(z)$ or $p(z_\lambda)$ = $p(x_t|x_0)$
- $q(z_{\lambda'}|z_\lambda,x) = q(x_{t-1}|x_t,x_0)$ ⇒ reverse process
- $z_{\lambda'} = x_{t-1}$ & $z_\lambda=x_t$
- $p_\theta(z_{\lambda_{min}})=p_\theta(x_T)=N(0,I)$
- $z_{\lambda_{min}} = x_T$ & $z_{\lambda_{max}}=x_1$
- $x_\theta(z_\lambda)=x_\theta(x_t, t)$
[SDE]
- If $x_\theta$ is corret, $T$→$\infty$로 보내면 $p(z)$의 sample paths를 가지는 SDE로 sampling 가능
- $p_\theta(z)$를 continuous time model distribvtuion으로 denote
- objective
- $\epsilon \sim N(0,I)$, $z_\lambda=\alpha_\lambda x+ \sigma_\lambda \epsilon$
- $\lambda \sim p(\lambda)$, over $[\lambda_{min}, \lambda_{max}]$
- $p(\lambda)$는 Uniform or not ⇒ 각각 효과 다름

- ⇒ Denoising score matching over multiple noise scales의 objective
- In paper ⇒ cosine noise schedule에 영감
- [Infinite timestep]
- $\lambda=-2logtan(au+b)$, $u \sim U(0,1)$
- $b =arctan(e^{-\lambda_{max}/2})$
- $a=arctan(e^{-\lambda_{min}/2})$
- [Finite timestep]
- $\lambda$는 corresponding to $U(0,1)$
- loss for $\epsilon_\theta(z_\lambda)$ - denoising score matching for all $\lambda$
- $\epsilon_\theta(z_\lambda)$ - model이 학습하는 score ft
- noisy data $z_\lambda$의 gradient of the log-density of the distribution의 estimate을 학습
- $\nabla_{z_\lambda}logp(z_\lambda)$, score ft
- 확률 density가 높은 영역으로 이동하면서, noisy data를 원래 데이터로 되돌리려는 역할
- $\sigma_\lambda$ - noise의 표준편차 ⇒ 각 $\lambda$시점에서의 noise 강도

- noise강도를 scale ⇒ noisy 데이터가 원래 데이터 분포로부터 얼마나 벗어났는지의 value
- But, unconstrained NN을 사용하기 때문에 any scalar potential이 존재 X
- ⇒ gradient 자체를 NN이 직접 학습할 수 o
- Sampling, learned diffusion model과 Langevin diffusion은 닮음
- $p(z_\lambda)$들을 sequence하게 sampling하여 $p(x)$로 converges
- $\epsilon_\theta(z_\lambda)$ - model이 학습하는 score ft
- Conditional generative modeling - $\epsilon_\theta(z_\lambda,c)$
- reverse process function approximator만 c를 추가로 input하고 나머지 동일
3. Guidance
- diversity of the samples 감소 ⇒ quality of each individual sample 증가
- Truncation in BigGan & Low temperature sampling in Glow
- ⇒ straightforward attempts in diffusion은 ineffective
3.1 Classifier Guidance
- Diffusion score $\epsilon_\theta(z_\lambda,c)$를 modify

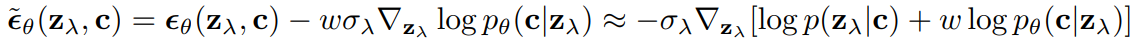
- ⇒ auxiliary classifier model $p_\theta(c|z_\lambda)$의 gradient of the log likelihood
- Modified score $\tilde\epsilon_\theta(z_\lambda, c)$가 $\epsilon_\theta$대신 sampling에 들어감
- approximate samples from 아래 distribution

- w - classifier $p_\theta(c|z_\lambda)$에 correct label에 대한 high likelihood를 assign하는 효과
- ⇒ IS of peceptual quality가 높아짐

- guidance 적용 안할 때, 3 class의 condition distribution ⇒ isotropic Gaussian distribution
- Isotropic Gaussian
- covariance matrix가 scale과 identity matrix로 표현되는 multivariate gaussian
- 방향과 상관없는 성질
- Isotropic Gaussian
- guidance를 적용하면 ⇒ non-Gaussian dist
- guidance strength 증가 ⇒ each conditional palaces mass는 서로 멀어지고, smalle regions에 concentrate됨
⇒ ImageNet model의 classifier guidance strength를 증가하여 IS boost & diveristy decrese
- IS score의 Inception v3은 ImageNet으로 pretrained
- Theoretically
- w+1의 classifier guidance to an unconditional model $\approx$ w의 classifier guidance to an condtional model


- ⇒ But, condtional model이 실험적으로 best results
- In this paper, guiding an already conditional model
3.2 Classifier-free guidance
- CFG -alternative method of modifying $\epsilon_\theta(z_\lambda,c)$
- score estimator $\epsilon_\theta(z_\lambda)$를 통해 parameterize된 Unconditional denoising diffuion model $p_\theta(z)$
- $\epsilon_\theta(z_\lambda,c)$를 통해 parameterize된 conditional model $p_\theta(z|c)$
⇒ 하나의 NN으로 both models를 parameterize
[Training]
- unconditional model은 class identifier c에 null token $\varnothing$ input ⇒ $p_{uncond}$확률 이용

- separate training 가능 but training pipeline이 복잡해지기 때문에, joint training

$x_t=\sqrt{\alpha_t}x_0+\sqrt{1-\alpha_t}\epsilon$
$\epsilon_\theta(x_t, c)$
[Sampling]
- linear combination of the cond/unconditional score estimates 사용
- no classifier gradient present

- $\tilde{\epsilon_\theta}$ - unconstrained NN 사용 ⇒ non-conservative vector fields인 score estimates을 construct함
- classifier gradient로 설명될 수 없는 vector fields

$x_T$
$\tilde{\epsilon_t}=(1+w)\epsilon_\theta(x_t,c)-w\epsilon_\theta(x_t)$
[Eq 의미]

- $\tilde{\epsilon_\theta}(z_\lambda, c)=\epsilon_\theta(z_\lambda,c) + w[\epsilon_\theta(z_\lambda,c)-\epsilon_\theta(z_\lambda)]$
- ⇒ implict classifier의 gradient처럼 두 score의 차이 form 사용
- 해당 equation은 classifier 존재 X
- But Implicit classifier에 영감받음 ⇒ $p^i(c|z_\lambda) \propto \frac{p(z_\lambda|c)}{p(z_\lambda)}$
- If exact score $\epsilon^*(z_\lambda,c), \epsilon^*(z_\lambda)$ 접근 ⇒ 이는 각각 $p(z_\lambda|c)$와 $p(z_\lambda)$의 score
- 이 score는 prob dist의 gradient로 계산
- $\nabla_{z_\lambda} \log p^i(c | z_\lambda) = -\frac{1}{\sigma_\lambda} \left[ \epsilon^*(z_\lambda, c) - \epsilon^*(z_\lambda) \right]$ : implicit classifier의 gradient
- classifier의 gradient는 $p(z_\lambda|c)$와 $p(z_\lambda)$의 score 차이로 구성
- implicit classifier인 classifier guidance는 score estimate을 아래처럼 수정
- $\tilde{\epsilon}^*(z_\lambda, c) = (1 + w)\epsilon^*(z_\lambda, c) - w\epsilon^*(z_\lambda)$
- $\tilde{\epsilon}^*(z_\lambda, c) = \epsilon^*(z_\lambda, c) + w[\epsilon^*(z_\lambda, c) - w\epsilon^*(z_\lambda)]$
- Eq(6)과 유사하지만, 근본적으로 다름
- $\tilde{\epsilon}^*(z_\lambda, c)$ - exact score estimate을 기반 ⇒ exact classifier gradients로 구성
- $\tilde{\epsilon_\theta}(z_\lambda, c)$ - NN으로 추정한 score estimate
- ⇒ Unconstrained NN으로 score를 estimate얻기 때문에, any classifier의 gradient아님
- Bayes’rule을 통해 얻은 implicit classifier가 guidance signal로 useful할지는 not obvious
- discriminative models이 보통은 implicit classifiers보다 outperform
- ⇒ But empirically CFG가 FID & IS의 trade off를 할 수 있음을 보여줌
4. Experiments
- CFG가 FID/IS tradoff를 attain하는지 & CFG의 behavior를 understand하기 ⇒ Purpose
- CG의 model architectures와 hyperparameters 그대로 사용
- ⇒ CG의 optimal이므로 CFG에 suboptimal일 수 o
- cond/unconditional models을 동일 architecture에서 진행하여 model capacity는 CG보다 낮음
- Nevertheless, competitive sample quality metrics & outperform prior work
- ADM - CG논문의 ablated diffusion model
- ADM-G - ADM + classifier guidance
4.1 Varying the classifier-free guidance strength
- figure & table
- ⇒ increasing cfg strength has the expected effect of decreasing sample variety and increasing individual sample fidelity
- 128x128 ImageNet의 results는 state of the art
- $w=0.3$, FID는 ADM-G보다 outperform
- $w=4.0$, BigGAN-deep의 최상 IS score일 때, FID & IS 모두 outperform
4.2 Varying the unconditional training probability
- CFG의 main hyperparameter at training time ⇒ $p_{uncond}=0.1$이 최적
- joint training때, unconditional generation의 훈련 확률
- $p_{uncond}$ - 0.5보다 0.1/0.2에서 IS/FID 모두 better
- sample quality를 위해서 model capacitiy의 작은 부분에만 unconditional generation task dedicate
4.3 Varying the number of sampling steps
- Sampling steps T: diffusion model의 sample quality의 major impact
- T- 128, 256, 1024
- ⇒ 증가할수록 sample quality improve & T=256이 sample quality와 speed의 balance good
- CG에 비해 sampling step은 cond/unconditional $\epsilon_\theta$ 2배
5. Discussion
- Diffusion models - Unconstrained NN으로 parameterize
- ⇒ score estimats가 conservative vector fields의 형태로 form X
- 다양한 방향으로 변화를 표현 o
- 다양한 데이터에 더 잘 generalize o
- 특정 규칙 X ⇒ sampling과정 더 유연하여, 데이터 분포에 가까운 샘플 생성 o
- ⇒ score estimats가 conservative vector fields의 형태로 form X
- pure generative models로 IS boosting을 demonstrate
- guidance 작동 ⇒ contional likelihood가 증가하고, unconditional likelihood of sample이 감소
- $-\epsilon_\theta(z_\lambda)$인 negative score term으로 인해 unconditional likelihood가 감소하기 때문
- ⇒ Not explored
- only a few classes의 경우 uncondtional score를 training하는 대신 condtional score로 $p(x)$사용 가능
- 많은 forward passes 발생 but CFG의 단점인 각 step 2번 sampling 과정을 없앨 수 o

[Future work]
- conditioning을 network 후반에 inject하는 architecture로 sampling 속도 증가를 완화 가능
- diversity를 유지하면서 fidelity 증가시키는 method 연구



