- Diffusion model 공부를 시작할 때, 관련 논문을 먼저 보는 것보다 해당 survey논문을 보는 것이 이해하기 편했음
- 해당 논문은 Class conditional diffusion model까지 수식적으로 잘 정리되어 있는 논문
- 해당 논문의 DDPM의 부분만 3가지 post로 나누어 정리할 예정
- (1) - Intro, ELBO, VAE, HVAE
[논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (1)
[논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (1)
Diffusion model 공부를 시작할 때, 관련 논문을 먼저 보는 것보다 해당 survey논문을 보는 것이 이해하기 편했음해당 논문은 Class conditional diffusion model까지 수식적으로 잘 정리되어 있는 논문해당 논
kongshin00.tistory.com
- (2) - Diffusion model(VDM), Maximizing ELBO 2가지
[논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (2)
[논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (2)
Diffusion model 공부를 시작할 때, 관련 논문을 먼저 보는 것보다 해당 survey논문을 보는 것이 이해하기 편했음해당 논문은 Class conditional diffusion model까지 수식적으로 잘 정리되어 있는 논문해당 논
kongshin00.tistory.com
- (3) - ELBO의 3가지 term - Reconstruction term, Prior matching term, Denoising matching term 의미 파악
[논문]
Understanding diffusion models: A Unified Perspective
https://arxiv.org/abs/2208.11970
Citations: 387
VDM
- ELBO2 decomposition


⇒ ELBO2의 denoising matching term optimize 의미파악이 목표!
Goal 1
$q(x_{t-1} | x_t, x_0)$를 forward process 값으로 유도

⇒ Bayes rule
- $q(x_{t-1} | x_t, x_0)$ - enconder의 Gaussian transtitions assumption 사용

- $q(x_t|x_0)$ & $q(x_{t_1}|x_0)$ - VDM의 encoder transitions 활용하여 linear Gaussian models로 다룰 수 있음
⇒ Reparameterization trick
- $x_t \sim q(x_t|x_{t-1})$, $x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}\epsilon$, $\epsilon \sim N(0, I)$
- $x_{t-1} \sim q(x_{t-1}|x_{t-2})$, $x_{t-1} = \sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon$, $\epsilon \sim N(0, I)$
- $x_t \sim q(x_t|x_0)$

⇒ $x_t \sim N(\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)I)$
- $x_{t-1} \sim q(x_{t-1}|x_0)$
⇒ $x_{t-1} \sim N(\sqrt{\bar\alpha_{t-1}}x_0, (1-\bar\alpha_{t-1})I)$
- $q(x_{t-1} | x_t, x_0)$에 1, 2 대입

⇒ $x_{t-1} \sim q(x_{t-1}|x_t, x_0) = N(\mu_q(x_t,x_0), \Sigma_q(t))$
- $\sigma^2_q(t) = (1-\alpha_t)(1-\bar\alpha_{t-1}) / 1-\bar{\alpha_t}$

- $\alpha$ ⇒ each timestep t에서 known & fixed
- pre-define된 hyperparameter로 설정
- model network의 output으로 설정
Goal 2
match $p_\theta(x_{t-1}|x_t)$ & $q(x_{t-1}|x_t, x_0)$ ⇒ ELBO2의 denoising matching term

- $q(x_{t-1}|x_t, x_0)$: ground-truth denoising transition step
- $p_\theta(x_{t-1}|x_t)$: approximate denoising transition step, Gaussian modeling
- $q(x_{t-1}|x_t, x_0) \sim N(\mu_q(x_t,x_0), \Sigma_q(t))$

- $p_\theta(x_{t-1}|x_t) \sim N(\mu_\theta(x_t,t), \Sigma_q(t))$
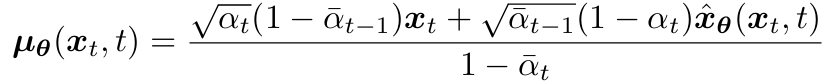
- ⇒ match $\mu_q(x_t, x_0)$ & $\mu_\theta(x_t,t)$
- ⇒ $p_\theta(x_{t-1}|x_t)$는 $x_0$에 condition X ⇒ $x_0$ 대신 $\hat{x_\theta}(x_t,t)$
- ⇒ $\alpha$는 t에 따라 고정된 값이므로 $\Sigma_q$ 동일
- KL Divergence between two Gaussian distributions

- two Gaussians의 variance 정확히 동일 ⇒ Optimizing $D_{KL}$은 두 분포의 mean 차이를 minimize
- $D_{KL}$ optimize ⇒ $\mu_{\theta}(x_t, t)$ & $\mu_q(x_t,x_0)$ match하도록 optimize
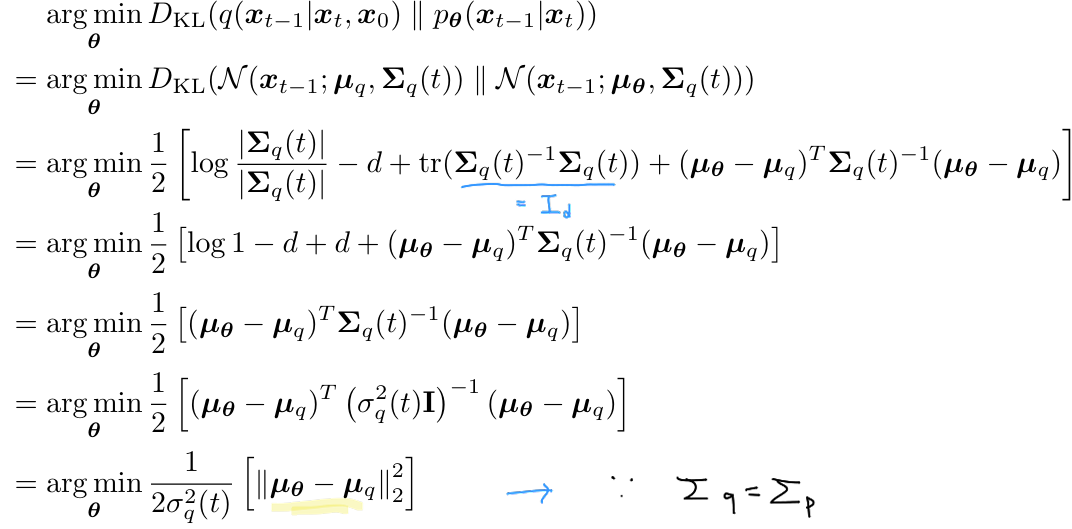

⇒ $\hat{x_\theta}(x_t,t)$ - parameter $\theta$와 Neural Network를 이용하여 $x_t$, $t$로부터 $x_0$를 예측하도록 학습
- Optimizing VDM - 임의의 노이즈된 이미지에서 original image($x_0$)로 예측하는 NN을 학습

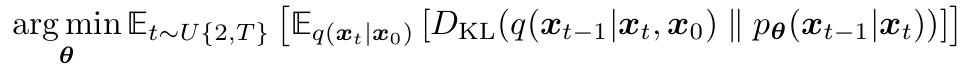
- Minimizing Summation term ⇒ Minimizing t에 대한 expectation로 approximate
- t ~ U(2,T) stochastic samples & sample t에 대한 $E_{q(x_t|x_0)}[D_{KL}]$ minimize하는 학습 진행
- 각 시간 단계에 대해 무작위 샘플을 추출, 해당 샘플을 사용하여 전체 목적함수를 최적화하는 과정
Equivalent Interpretation
- $x_0$를 다른 방법의 equivalent parameterizations ⇒ VDM의 다른 해석
⇒ Reparameterization trick

- $x_t, \epsilon_0$을 알면 $x_0$를 알 수 o ⇒ $\hat{\epsilon_{\theta}}(x_t, t)$가 $\epsilon_0$ 근사하도록 학습
- $\mu_q(x_t, x_0)$ : true denoising transition mean

- $\mu_\theta(x_t, t)$: approximate denoising transition mean

- KL Divergence between two Gaussian distributions

- $\hat{\epsilon_\theta}(x_t, t)$ - $x_0$ → $x_t$를 결정하는 source noise $\epsilon_0 \sim N(0, I)$를 예측하도록 학습하는 NN
- original image $x_0$를 예측하도록 VDM 학습 = noise를 예측하도록 VDM 학습
⇒ Empirically, noise를 예측하도록 학습하는 것이 better performance
'Paper Review > 2D Diffusion Model' 카테고리의 다른 글
| [논문 리뷰] DDIM: Denoising Diffusion Implicit Models (2) | 2025.03.18 |
|---|---|
| [논문 리뷰] DDPM: Denoising Diffusion Probabilistic Models (0) | 2025.03.18 |
| [논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (2) (0) | 2025.03.16 |
| [개념 설명] Reparameterization Trick (0) | 2025.03.16 |
| [논문 리뷰] VDM survey: Understanding diffusion models: A Unified Perspective (1) (0) | 2025.03.16 |



