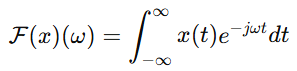[개념 설명] DPS와 DPnP 비교

• Diffusion Posterior Sampling 방법과 Diffusion plug-and-play method에 대해 이론적, 실험적 비교를 위한 post
• DPS 논문 리뷰

 [논문 리뷰] DPS: Diffusion posterior sampling for general noisy inverse problems

[논문 리뷰] DPS: Diffusion posterior sampling for general noisy inverse problems

 

• DPnP 논문 리뷰

[논문 리뷰] DPnP: Provably Robust Score-Based Diffusion Posterior Sampling for Plug-and-Play Image Reconstruction

[논문 리뷰] DPnP: Provably Robust Score-Based Diffusion Posterior Sampling for Plug-and-Play Image Reconstruction

 

---

[DPS]

• Classifier guidance와 동일하게 bayes’ rule를 사용하여 uncond.부분과 $p(y|x_t)$를 통해 posterior sampling 진행
• $\nabla_{x_t}logp(x_t|y)=\nabla_{x_t}logp(x)+\nabla_{x_t}logp(y|x_t)$
• $p(y|x_t)$를 $p(y|\hat x_0)$로 approx.하여 general forward model의 첫 posterior sampler 제안

[Denoising posterior sampler DDS (DPnP)]

• data x를 low-dim manifold $\mathcal M$에 위치시킴 ⇒ $logp^\star(x)=-\infty, x\notin\mathcal M$

 

• 기존 Algorithms들은 proximal operator에서 conditional expectation map을 사용
  •  

    

     

  • 

  • 
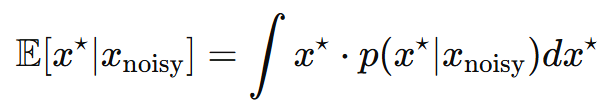
  • $p(x^\star|x_{noisy})$를 계산할 때 $x^\star$에 대한 가중평균 형태로 계산
  • $\mathcal M$이 nonlinear할 경우, $\mathcal M$에 떨어진 point를 생성할 수 있음 ‘
    • ⇒ prior constraint 위반하여 reconstruction quality 저하

 

• ⇒ but DDS는 $p^\star(x)$에서 직접 sampling하기 때문에 prior constraint를 더욱 잘 유지

 

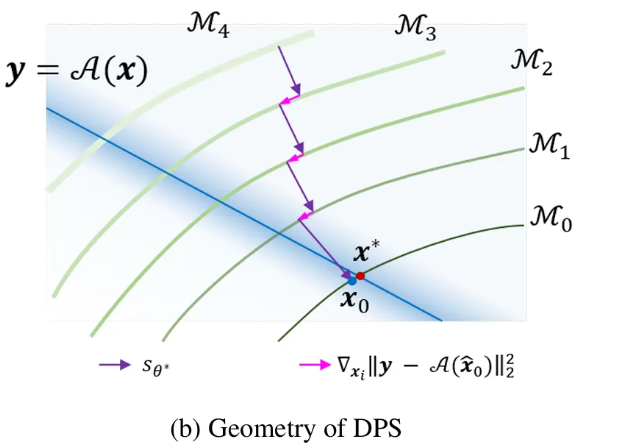
• DPS - $s_{\theta^\star}$ 한 step 이동 후 $p(y|\hat x_0)$의 gradient로 한 step 이동
• DPnP - 단순히 각각의 step 이동이 아닌 proximal term을 통해서 2가지 constraint에 벗어나지 않게 설정

---

Numerical experiments

• 3가지 linear and nonliear inverse problems

 

1. Phase Retrieval

• Fourier 변환된 data에서 위상 정보 복원
• image($x$) & random mask($M$) - 256 x 256
• Fourier transform $\mathcal F$ - $\mathcal F(x)=|\mathcal F(x)|e^{j\phi(x)}$
  • 
• Forward operator - $A(x) = \text{mag}(\mathcal{F}(M \odot x))$
• $mag$ - magnitude of a matrix with complex entries
• $\xi\sim N(0,0.2)$

 

2. Quantized sensing

• low-bit(1bit) quantized version으로부터 image 복원
• Forward operator - 각 channel의 각 fixel에 대해 $Q$ 적용

  • 

     
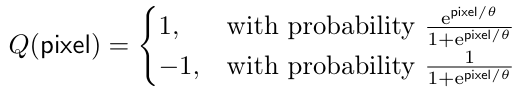
  • pixel $\in[-1,1]$, $\theta=0.4$
  • ⇒ channel 별 1bit의 image 생성 (기존 8bit)

 

3. Super resolution

• row resolution으로부터 high resolution image 복원
• Forward operator - Bicubic downsampling operator(4:1)
  • linear operator & $\xi\sim N(0, 0.2)$

 

[Results]

• DPS: Diffusion Posterior Sampler
• LGD-MC: Loss-Guided Diffusion with Model Carlo approach
• Visual results
  • DPnP - linear and nonlinear problems 해결 가능 & SOTA (선명 & detail 복원)

 

• Performance metric
  • LPIPS - Learned Perceptual Image Patch Similarity
    • VGG network 여러 layer에서 추출된 feature vector 비교 ⇒ 낮을수록 good
  • PSNR - Peak Signal-to-Noise Ratio
    • fixel 단위 차이를 측정하는 지표 ⇒ 클수록 good
    • $PSNR = 10*log_{10}(\frac{MAX^2}{MSE})$

 

1. FFHQ - 256 x 256
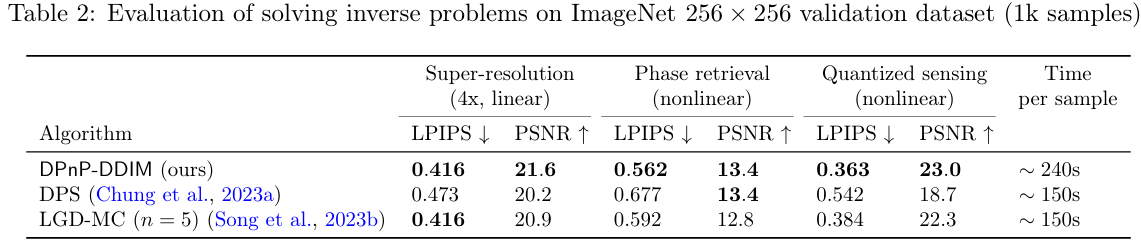
   •   모든 problems에서 성능 우수
   •   1.5x computation time 필요
   • 
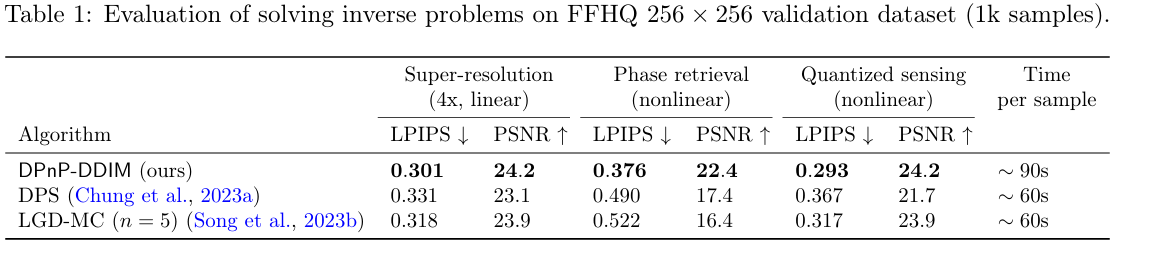
2. ImageNet - 256 x 256
   • 

 

[DPnP]

• Diffusion Plug and Play
• Score-based diffusion model의 image prior와 general forward model을 결합하여 posterior sampling
  • ⇒ Nonlinear inverse problem문제 해결